
1.掌握枚举算法的基本模型。
2.体验基于枚举算法解决问题的基本过程,感受计算机编程的魅力。

熟练掌握枚举算法的综合应用。

安装有Python软件且连网的计算机。

![]()
![]()
项目情景:“模糊的票据数字”
一张文具采购的票据上,金额数(4位数)的十位数字部分不小心沾上了墨水,模糊显示为“12*1”元,但已知此4位数能被21整除,那么如何推算出这张票据的真实金额数字?
![]()
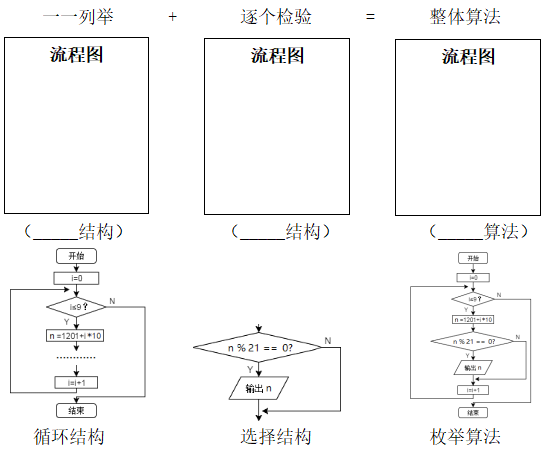
教师根据学生回答的情况,总结出解决此问题的思路:在1201~1291的范围内,找出个位数是1且能被21整除的数。其中利用了枚举算法思想。
即在一定范围内(1201~1291)列举出所有可能(个位数为1且能被21整除)的情况的方法。强调枚举算法的三要素:对象、范围、验证条件。
![]()
小组分工实践:
学生以小组为单位,进行讨论并分工合作。利用枚举算法,一起完成“模糊的票据数字还原”的程序实现。建议以“分析à设计à编程à调试à完善”的步骤进行。
问题分析
(1)本问题求解目标是:票据金额具体数字
(2)已知条件是:4位数字其中3位已知12*1,且此数能被21整除
(3)已知与未知的关系:要求解的票据金额必须满足已知条件
设计算法
(1)剖析方案:
根据问题分析,只要将所有可能的数一一列举,然后逐个检验是否符合条件,就可以找到数字。
(2)算法要点:完成表格,并与同组成员相互比较思路的异同
对象 | 条件 | |
列举 | ||
检验 |
(3)流程图绘制:
编程调试

交流完善
小组交流。各小组交流程序实现情况以及存在的问题,通过算法和语法的分析,整合完善代码。
ython程序: |
参考代码:

![]()
小组合作分析算法,编写程序:按照票据上的金额购买7元和15元的两种笔筒,要求必须将金额使用完毕,有几种购买方案?
在此过程中解决以下问题:
(1)是否可能存在多解?如何存储多个解?
(2)本问题需要枚举几个变量?设置几重循环?
(3)如何减少枚举变量的范围以提高效率?
(4)如何减少枚举变量的数量以提高效率?
ython程序: |
视频:“笔筒购买”问题
![]()
材料“果农的烦恼”:已到新鲜水果上市季节,面对大量采摘下的苹果,果农们开始发愁了,人工费贵不说,工人也请不到;考虑天气因素,水果在仓库多放几天或保存不当容易坏;如果直接卖出去,因为果子品质参次不齐,价格低迷还容易落下不好的碑,请同学们帮忙设计一个程序,帮果农快速地挑选出好苹果。
学生小组合作讨论并实践,编程分拣仓库里的苹果。
过程记录 | 步骤一: |
步骤二: | |
步骤三: | |
步骤四: | |
分享心得 | |
![]()
个人评价表
知识与技能 | 评价等级 | |||
A | B | C | ||
理解枚举算法的含义及特征 | ||||
掌握枚举算法的建模 | ||||
掌握枚举算法流程图的绘制 | ||||
独立编写代码实现算法 | ||||
熟悉枚举算法并提出优化方案 | ||||
情感态度与价值观 | 评价等级 | |||
A | B | C | ||
学习态度 | 态度认真,参与自主学习 | |||
合作意识 | 积极参与小组讨论与合作 | |||
组织能力 | 承担信息整合、总结任务 | |||
注:A=非常符合,B=符合,C=不符合
组内成员互评表
评价内容 组员姓名 | 组员1 | 组员2 | 组员3 | 组员4 | ||||||||
对小组的探究内容献计献策 | A | B | C | A | B | C | A | B | C | A | B | C |
与小组成员和睦相处 | A | B | C | A | B | C | A | B | C | A | B | C |
很好地完成所负责的任务 | A | B | C | A | B | C | A | B | C | A | B | C |
积极参与小组活动 | A | B | C | A | B | C | A | B | C | A | B | C |
注:每一项评价内容A=非常符合,B=符合,C=不符合



